Les fonctions

Les fonctions au sens où on les connait ne sont pas celle de l’informatique.

Fonctions simples

Pour définir une fonction mathématique \(f:x \to x^3-2x^2-3x+5\), on écrit :

>>> def f(x):
...     return x**3-2*x**2-3*x+5
>>> f(0)
5
>>> f(10.5)
910.625

>>> t = linspace(0,10,11)       # On prend un tableau que l'on fait passer dans la fonction
>>> t
array([  0.,   1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.])
>>> f(t)                        # On récupère un tableau dont les éléments sont les images par la fonction du tableau précédent
array([   5.,    1.,   -1.,    5.,   25.,   65.,  131.,  229.,  365.,
545.,  775.])

Note

• L’oubli des deux points ":" après la première ligne est une erreur courante.
• L’oubli de l’indentation de la fonction à exécuter est aussi une erreur courante.

Nous proposons ici un fichier exemple pour tracer une fonction. Pour plus de détails, nous renvoyons le lecteur au chapitre concerné (Graphiques).

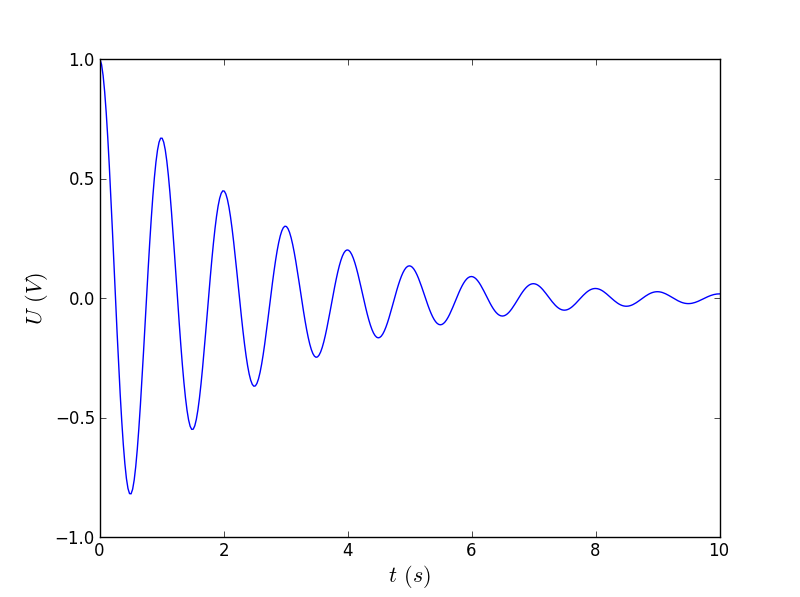
# -*- coding: utf-8 -*-

"""
Exemple de graphique de fonction
"""

from __future__ import division
from scipy import *
from pylab import *

t = linspace(0,10,400)                         # Temps = Abscisses

Q = 5                                          # Valeur du facteur de qualité
omega = 2*pi                                   # Valeur de la pulsation omega

def U(temps):
    return exp(-2/Q*temps)*cos(omega*temps)    # Fonction U dépendant de la variable temps

plot(t,U(t))                                   # Graphique

xlim(0, 10)                                    # Limites de l'axe des abscisses
xlabel(ur"$t \, (s)$", fontsize=16)            # Label de l'axe des abscisses

ylim(-1, 1)                                    # Limites de l'axe des ordonnées
ylabel(ur"$U \, (V)$", fontsize=16)            # Label de l'axe des ordonnées

show()

ce qui donne

On peut directement le télécharger.

Une fonction au sens de la programmation ne se limite pas à une entrée ou une sortie de nombre. On peut utiliser des chaînes de caractères ou tout autre type de variable en python, par exemple

>>> def Megalomanie(x):
...     print((u"J'aime " + x + u" ")*10)
>>> Megalomanie("Python")
J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python J'aime Python

Les arguments

Pour définir une fonction mathématique à plusieurs arguments (ou un argument et des paramètres) telle \(U:(t,\tau) \to e^{-t/\tau}sin(\omega t)\), on écrit une fonction avec autant de vraiables que nécessaire :

>>> from scipy import *
>>> omega = 2*pi
>>> def U(x,tau):
...     return exp(-x/tau)*sin(omega*x)

>>> t = linspace(0,10,11)
>>> T(t,5)
array([  0.00000000e+00,  -2.00531199e-16,  -3.28362120e-16,
-4.03260248e-16,  -4.40215422e-16,  -4.50522380e-16,
-4.42627833e-16,  -4.22791856e-16,  -3.95603079e-16,
-3.64378958e-16,  -3.31475843e-16])
>>> T(t,10)
array([  0.00000000e+00,  -2.21621250e-16,  -4.01062398e-16,
-5.44344398e-16,  -6.56724239e-16,  -7.42785831e-16,
-8.06520496e-16,  -8.51398244e-16,  -8.80430844e-16,
-8.96227618e-16,  -9.01044760e-16])

Ces fonctions peuvent aussi être tracées en fonction du paramètre (Voir le chapitre dédié)

Vectorisation d’une fonction

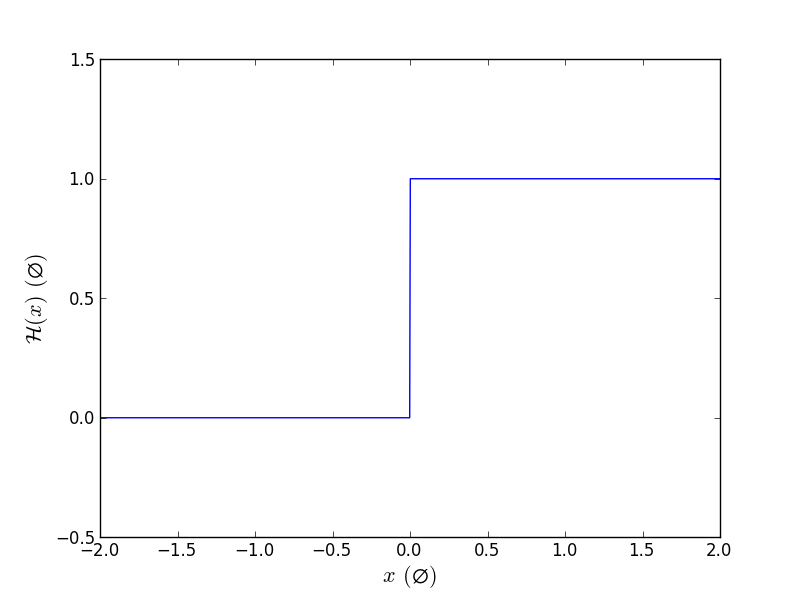
Lorsque la fonction fait appel à un test, il n’est pas possible d’utiliser un tableau comme argument d’une fonction. Un exemple d’une telle fonction est la fonction de Heaviside

\[\begin{split}\forall x \in \mathbb{R},\ \mathcal{H}(x)=\left\{\begin{matrix} 0 & \mathrm{si} & x < 0 \\ 1 & \mathrm{si} & x \ge 0. \end{matrix}\right.\end{split}\]

Si l’on code la fonction et que l’on essaye de passer un tableau en argument, on obtient :

>>> from scipy import *
>>> def f(x):
def f(x):
...     if x>=0:
...          res = 1
...     else:
...          res = 0
...     return res

>>> f(0)                        # Cette fonction marche pour des réels
1
>>> f(0.5)
1
>>> f(-0.5)
0

>>> x = linspace(-2.,2.,11)     # Mais pas pour les tableaux...
>>> f(x)
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

Python ne sait pas comment gérer la comparaison avec le tableau, il faut préciser que le test se fera élément par élément. Une fonction de Numpy (importé depuis Scipy) permet d’effectuer cette opération dite de vectorisation (vectorize()). Il s’agit d’une boucle for qui effectue la comparaison élément par élément. Pour plus de détails, on pourra se reporter à la documentation de Scipy p.12-13.

>>> f_vect = vectorize(f)       # Fonction "vectorisée"
>>> f_vect(x)
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1])

Une fois la fonction vectorisée tracée, voici le graphique obtenu :